円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう! 円柱の体積の公式 V=πr 2 hって? 円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率た円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデ
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
円柱 表面積 公式 小学生
円柱 表面積 公式 小学生-『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ円柱の表面積は (円柱の表面積)= 2×(円周率)×(底面の円の半径)×{(底面の円の半径)(高さ)} 円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。側面部分は筒状ですが、開いて四角形の状態 半径が6㎝なので (底面の円の面積)=(半径)×



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
円柱 の体積 の半分 が微小な幅であるとき,上の公式は次のことを表している. 原点を中心とする半径 の円を 軸のまわりに1回転してできる回転体の表面積を求める.左右対称だから右半分を求め まずは底面積 (S)を求めます。 「底面積=半径×半径×円周率」で計算できるので「6×6×π=36π (cm2)」が底面積です。 そして、底面積×高さ (h)=円柱の体積ですから、「36π×13=468π (cm3)」が答えです。 円柱の表面積の求め方の公式 をつかってしまえば2秒ぐらいで計算できちゃうんだ。 下の図のように、円柱底面の半径をr、高さをhとすると、 2πr(hr)
円柱の表面積の求め方 公式にして問題を素早く解く 苦手な数学を 簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを 円柱の表面積と体積を求める公式 具体例で学ぶ数学 公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを 計算公式よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積側面積 π (a b) (a − b) 2 h 2
円柱表面積公式 中学数学円錐の表面積の求め方と公式図たくさん 分数の連立方程式で分母が文字の場合の解き方解答3通り 中1数学方程式の問題-厳選15題レベル別・解説付き円柱の表面積を求める公式は、 S = 2πr^2 2πrh = 2πr(rh) で表されます。このページでは、例題と共に、円柱の表面積の求め方を説明しています。 つづいて柱体の表面積の求め方について見ていきましょう。 柱体は同じ形の『底面』とそれに挟まれた『側面練習131 球面x 2 y 2 z2 = a の表面積を求めよ。( z = p a ¡x2 ¡y2 の fx2 y2 • a2g 上の曲面積の2倍) 宿題131 1) 二つの円柱x2 y2 • a2, y2 z2 • a2 の共通部分の体積を求 めよ。(変数変換は必要ない) 2) 円柱面x2 y2 = a2, 平面z = 0, 曲面z = x2 y2 で囲まれた領域の体積 を



1




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
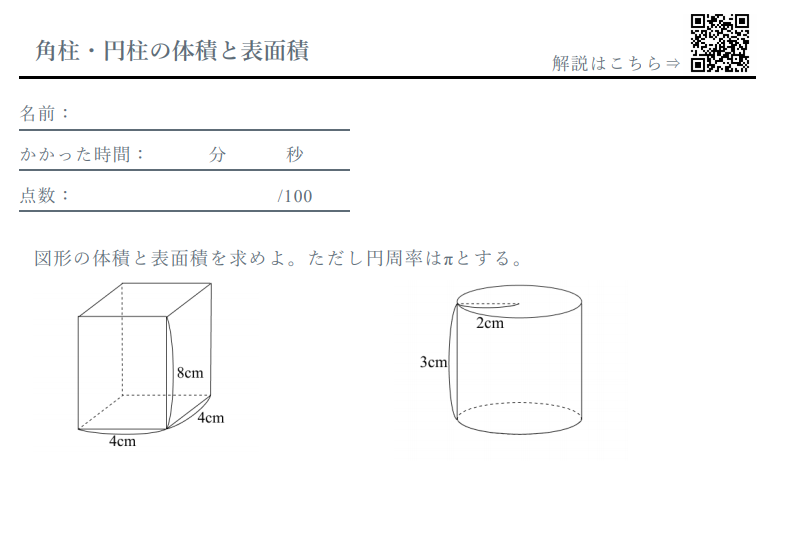
体積は32π($cm^3$)となります。 次に、円柱の表面積の求め方は「底面積 × 2 側面積」なので、式は「4π × 2 側面積」。 また、円柱の側面積の求め方は「高さ × 円周」、円周の求め方は「直径 × π」なので、式にすると 4π × 2 8 × 4π = 40π 円柱の体積の求め方に関しては、三角柱などの体積の求め方と変わりません。 〇〇柱の体積は、全て (底面積)× (高さ) で求まると覚えていて良いです。この公式に当てはめて、上の円柱の面積を求めると、 底面積=3×3×314 側面積=10×3×2×314 円柱の表面積=3×3×314×2+10×3×2×314




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



角柱 円柱の体積と表面積 計算ドリル 問題集 数学fun
表面積 = 2 × 173 × 一辺 × 一辺1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード 円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち 円錐の表面積や体積の求め方 すぐ分かる方法まとめ:「円柱の表面積の求め方」は公式なんかいらねえ! 円柱の表面積は公式を使えば2秒で計算できる。 だけれども、公式に頼らなくたって、5分ぐらいで計算できちゃうよね笑 円柱の体積、表面積の求め方はこれでバッチリ!←今回の記事




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




球の表面積と体積の公式 数学fun
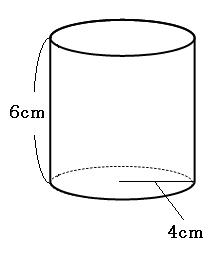
入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を導きます。 円柱の体積は半球の3倍(実験にて確認)円柱 円柱の表面積を求める公式は、次の通りです。 上の基本問題をこの公式を使って求める (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 小学生向けに、文字を使わずに書くと次のようになります。 側面の面積=6cm×8πcm=48πcm2直円柱の半径と高さから体積、側面積、表面積を計算します。 一部が欠けた直円柱の体積 一部が欠けた直円柱の体積 一部が欠けた横倒し直円柱の半径と高さから体積、側面積、底面積、上面積を計算し




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
これで上下の円と側面の面積を求めることができたので、これらを合計すれば円柱の表面積を求めることができます。 半径4cm・高さ6cmの円柱 ※円周率を314とした場合 円の面積=4cm×4cm×314=5024cm 2 円の円周=4cm×2×314=2512cm 側面の面積=6cm×2512cm=cm 2 円柱の面積=5024cm 2 5024cm 2 cm 2 =2512cm 2 ※円動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 円柱の体積、表面積の求め方はこれでバッチリ!←今回の記事 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!




立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




表面積一定の円柱と直方体の体積の最大値 理系のための備忘録
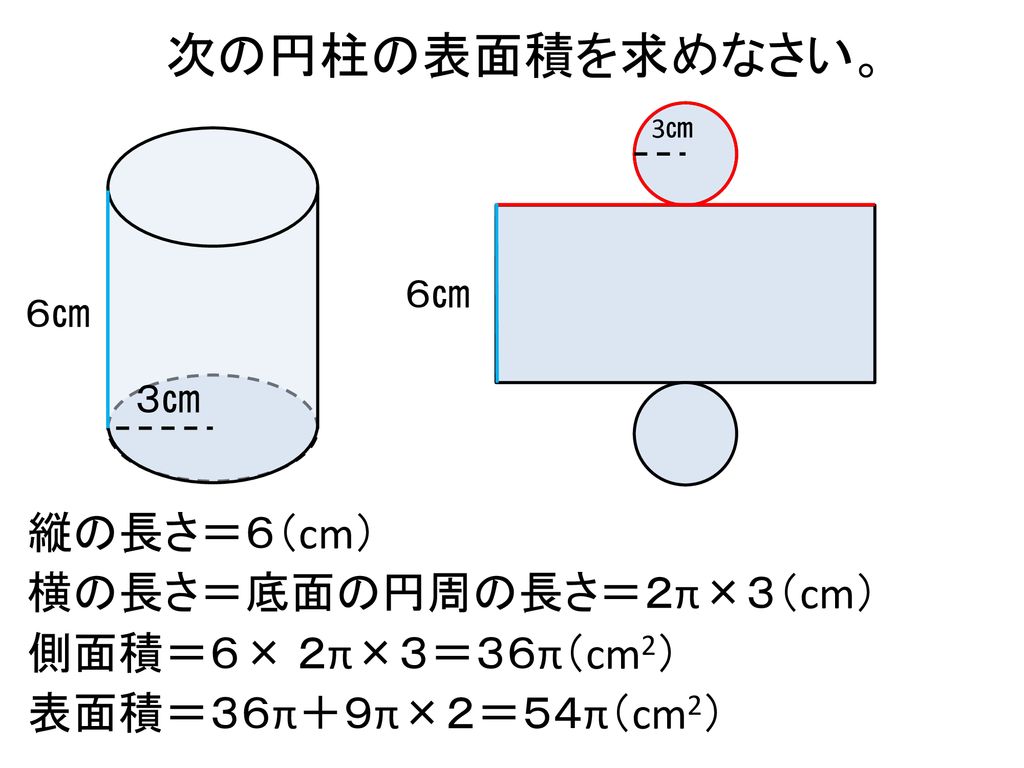
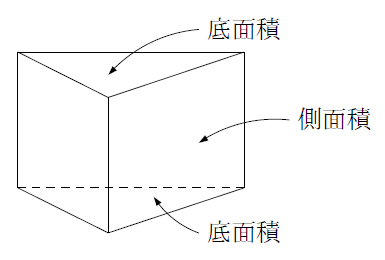
2角柱と円柱 角柱・円柱の體積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの體積=底面積×高さ× 1 3 角すいと円すいの表面積=底面積側面積 4円すいの展開図 側面のおうぎ形の中心角=360 × 底面の半徑角柱・円柱の表面積と体積の公式 管理人 2月 5, 19 / 2月 12, 19 主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。あとは、長方形の面積公式に従って(縦)×(横)を計算すればOKですね。 $$8\\times 12\\pi=96\\pi(cm^2)$$ 側面積を求めることができたので、表面積も求めておきましょう。 底面積が、\\(6\\times 6\\times \\pi=36\\pi(cm^2)\\)となるので 円柱の表面積を求める公式は、次の通りです。 円の面積=4cm×4cm×π=16πcm2



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
円柱の表面積の公式 底面の円の面積が \(S_1\)、円柱の側面積が \(S_2\) のとき、円柱の表面積 \(S_S\) は、次の式で求められる。 \begin{align}\color{red}{S_S = 2S_1 S_2}\end{align}球の体積や表面積と、その球がちょうど入る円柱の体積や側面積との関係を、計算結果等で 確かめ、イメージとしてもっておきましょう。 2( 1 )球の表面積を求める公式: S=4πr2 ( 2)円柱の底面の円の半径: r ,円柱の高さ: 2r (円柱の表面積を求める公式は、 S = 2πr^2 2πrh = 2πr(rh) で表されます。 このページでは、例題と共に、円柱の表面積の求め方を説明しています。 お使いのブラウザでは JavaScript が無効になってい




Catatan Tentang 体積 表面積 側面積 の公式 Junior Clear




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 + 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明します。 体積の求め方の詳細は 三角柱、四角柱、円柱の体積の求め方 に書いています。




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト




2 を途中式を含めて教えてください Clear
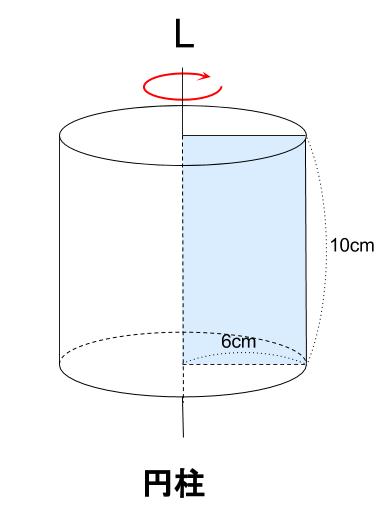



中学数学 回転体 その1 中学数学の無料オンライン学習サイトchu Su




角柱 円柱の表面積と体積の公式 数学fun
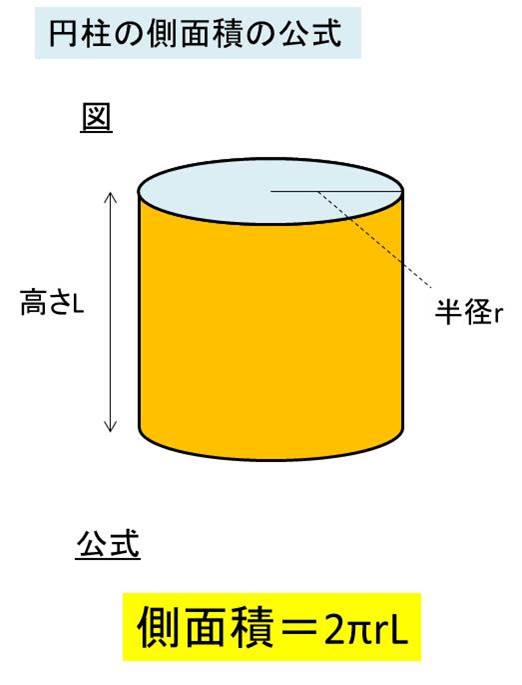



円柱の側面積 底面積 表面積を求める方法 モッカイ




初等幾何 球の表面積を求める 大人が学び直す数学




円柱の表面積 Youtube




円柱の体積 表面積 側面積 計算機 かんたん計算機




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
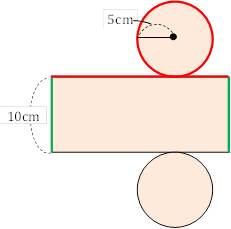



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



U9j580gf8iba369ji2w Xyz P 296



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




丸棒の重量 円柱の体積と重量の求め方 鉄の場合




側面 側面積とは 問題を解いて慣れよう 苦手な数学を簡単に




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




中学1年生 数学 無料問題集 角柱や円柱の表面積 おかわりドリル




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




円柱の体積の求め方 公式 小学生 中学生の勉強




円柱の表面積 Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
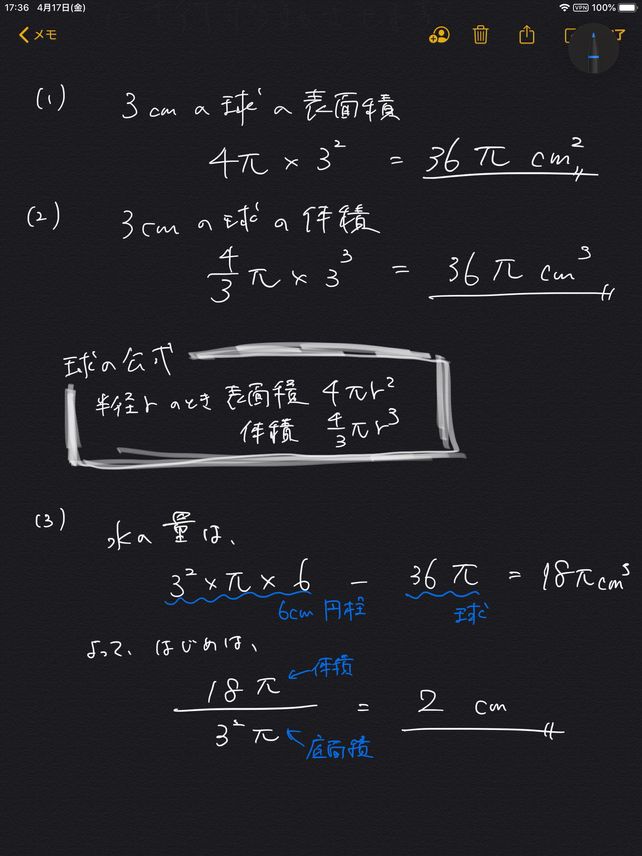



5 3cm 3cm6cm 1 Left 3ri Descubre Como Resolverlo En Qanda
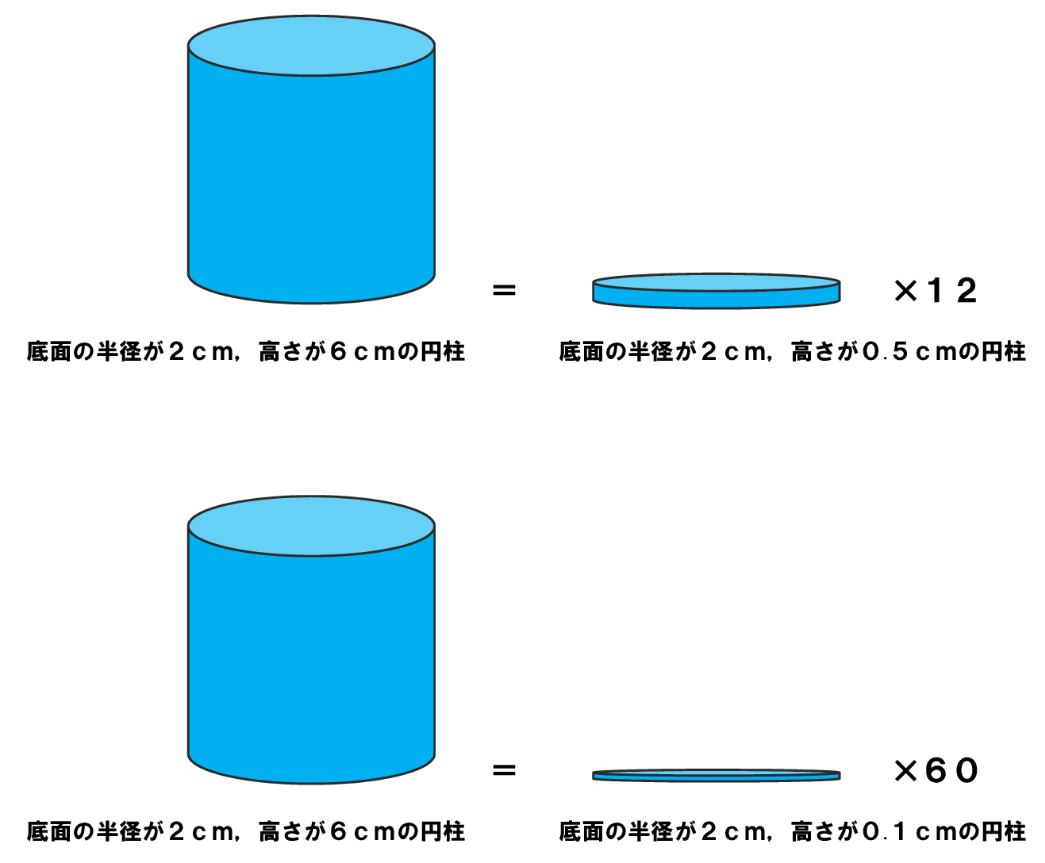



もたこ博士の算数工房 算数から数学まで



柱体とすい体 中学受験 田中貴 Com




中1 数学 6 2 角柱 円柱の表面積 Youtube
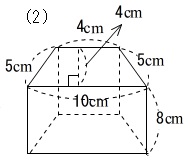



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球




体積 表面積




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




円柱の表面積と体積を求める公式 具体例で学ぶ数学



円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係




球の体積と表面積 公式と計算問題と証明 Irohabook




公式を図解 すい体の体積 円すいの表面積の求め方
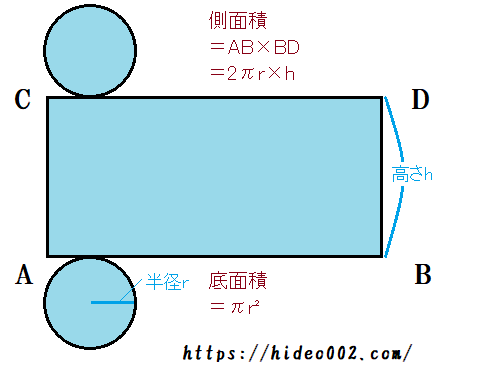



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋



1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋
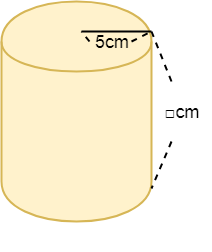



円柱の体積の求め方 公式 小学生 中学生の勉強




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
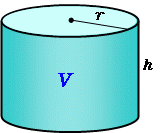



直円柱の体積 高精度計算サイト




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学1年生 数学 無料問題集 角柱や円柱の表面積 おかわりドリル




球の表面積と体積の公式 数学fun




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
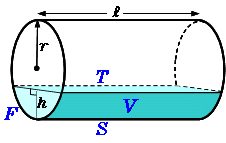



一部が欠けた直円柱の体積 高精度計算サイト




円柱の表面積 あんず学習塾のメモ 図表置き場




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




円柱の表面積の求め方 公式と計算例
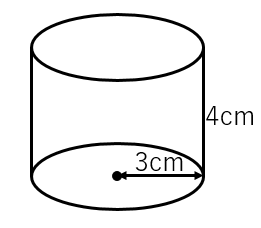



円柱の表面積と体積を求める公式 具体例で学ぶ数学




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



1



3



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
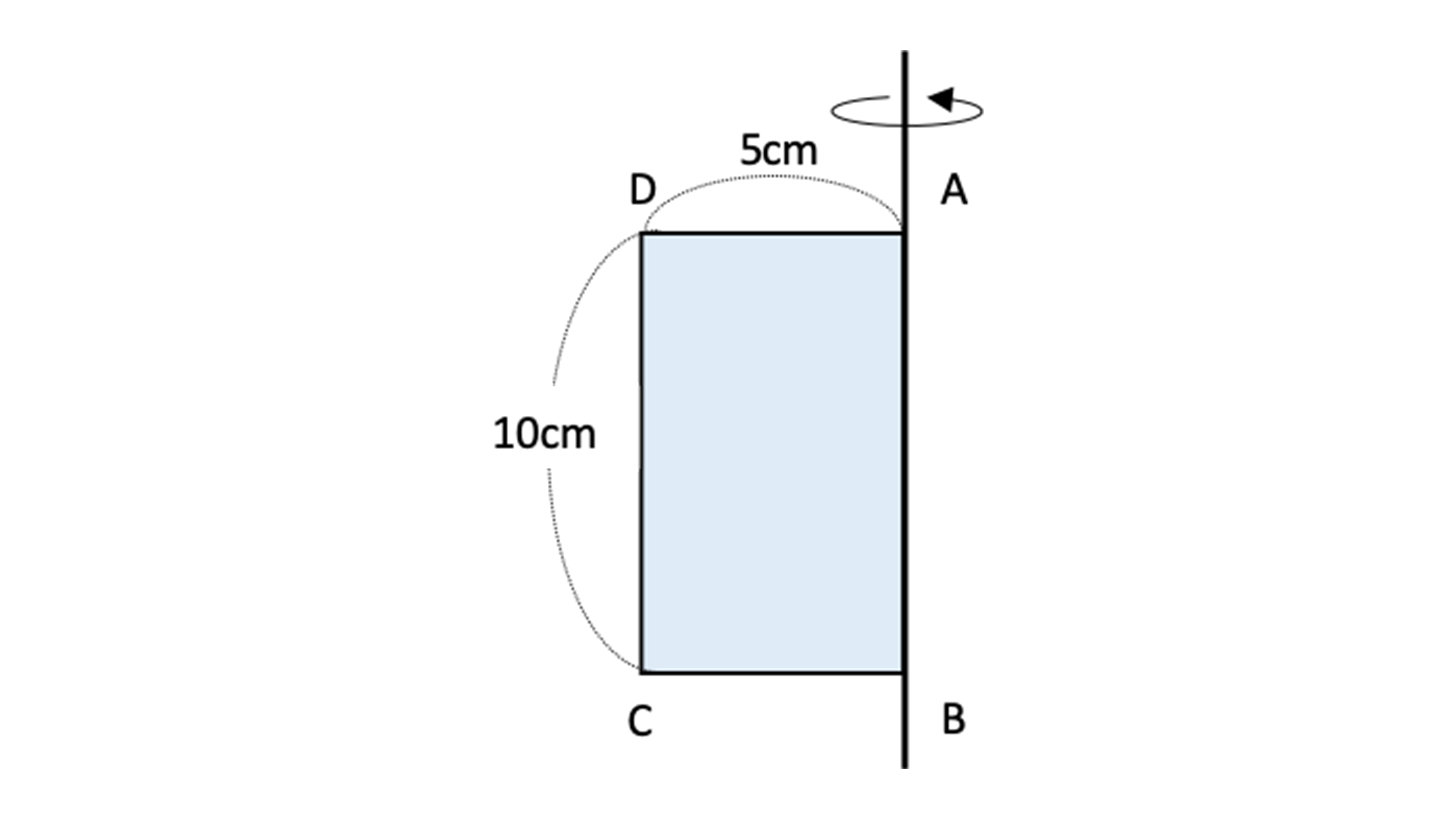



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



立体の表面積



Math 円柱 内接する球 円錐の体積と表面積 働きアリ



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download



角柱 円柱の表面積 まなびの学園




表面積の求め方 計算公式一覧



3




角錐 円錐の体積と表面積の公式 数学fun




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




表面積の求め方 計算公式一覧




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



円柱の表面積 簡単に計算できる電卓サイト




角柱や円柱の表面積の求め方を教えてください Clear



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円柱 P12




円柱の表面積の求め方 公式にして問題を素早く解く 苦手な数学を簡単に




スタディピア 立体の表面積




円柱の表面積の求め方 公式と計算例




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱の体積の求め方 公式 小学生 中学生の勉強
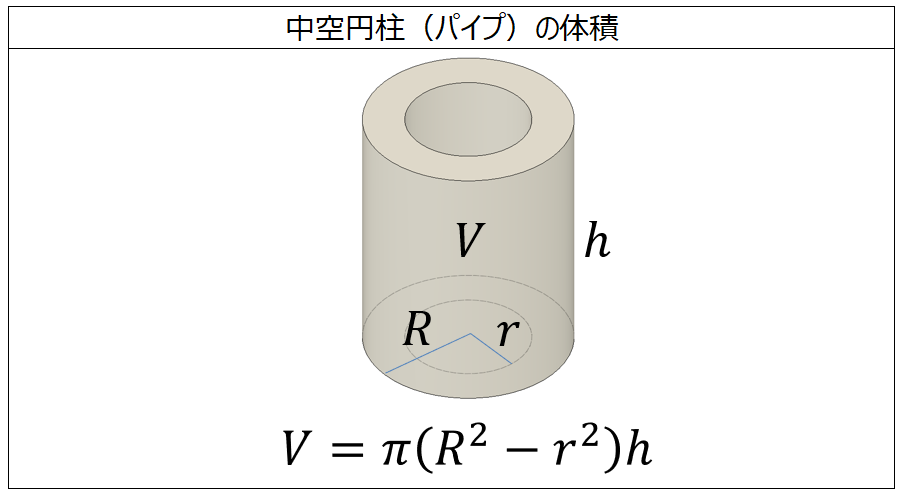



体積の計算 中空円柱 パイプ 製品設計知識




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿