Solve ( x 2 − y 2) d x 2 x y d y = 0 I'm asked to solve it using 2 different methods I proved I can find integrating factors of type μ 1 ( x) and μ 2 ( y / x) If I'm not wrong, these two integrating factors are μ 1 ( x) = x − 2 , μ 2 ( y / x) = ( 1 y 2 x 2) − 2 ∂ ψ ∂ x = x − 2 (
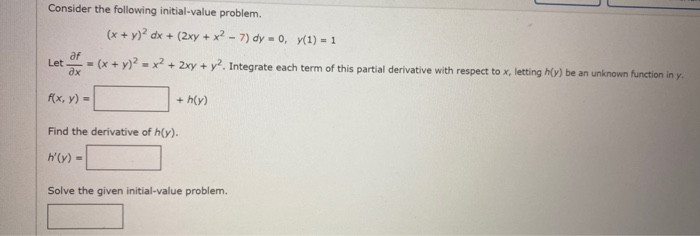
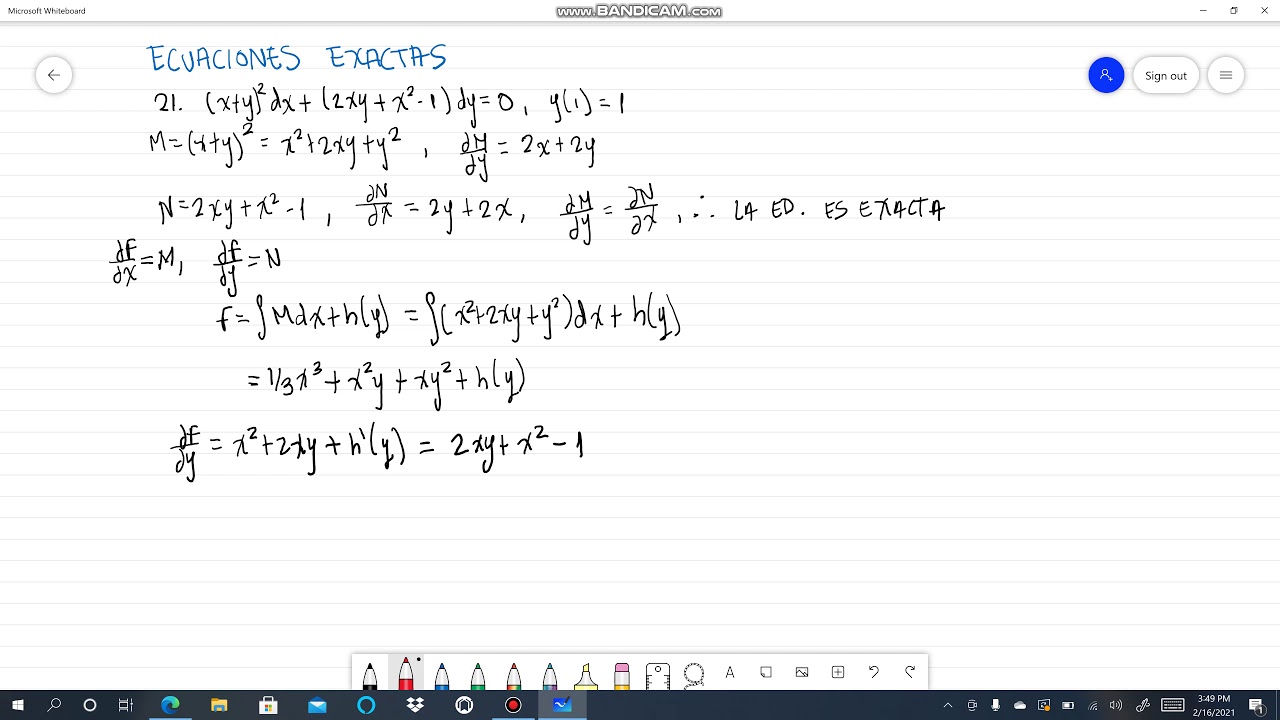
X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1- Ex 95, 4 show that the given differential equation is homogeneous and solve each of them ( ^2 ^2 ) 2 =0 Step 1 Find / ( ^2 ^2 ) 2 =0 2xy dy = ( ^2 ^2 ) dx 2xy dy = ( ^2 ^2 ) dx / = ( ^2 ^2)/2 Step 2 Putting F (x, y) = / and finding F ( x, y) F (x, y) = ( ^2 ^2)/2 F ( x, y) = ( ( )^2 ( )^2)/ (2 )= ( ^2 ^2 ^2 ^2)/ ( ^22 )= ( ^2 ( ^2 ^2))/ ( ^22 ) = ( ^2 ^2)/2 = F (x, y) F ( x, y) = F (x, y) = FFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep
X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
 |  | |
 | ||
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
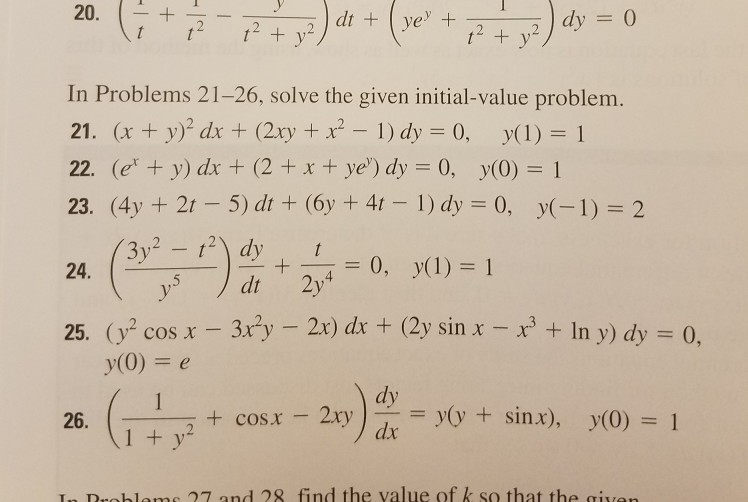 | ||
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
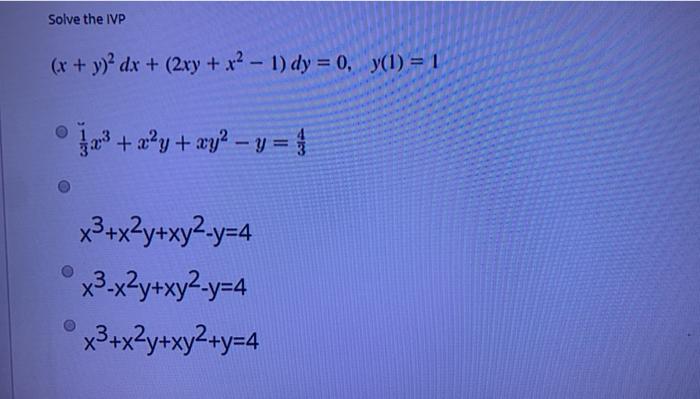 |  |  |
 | ||
 |  | |
 |  | |
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  | |
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
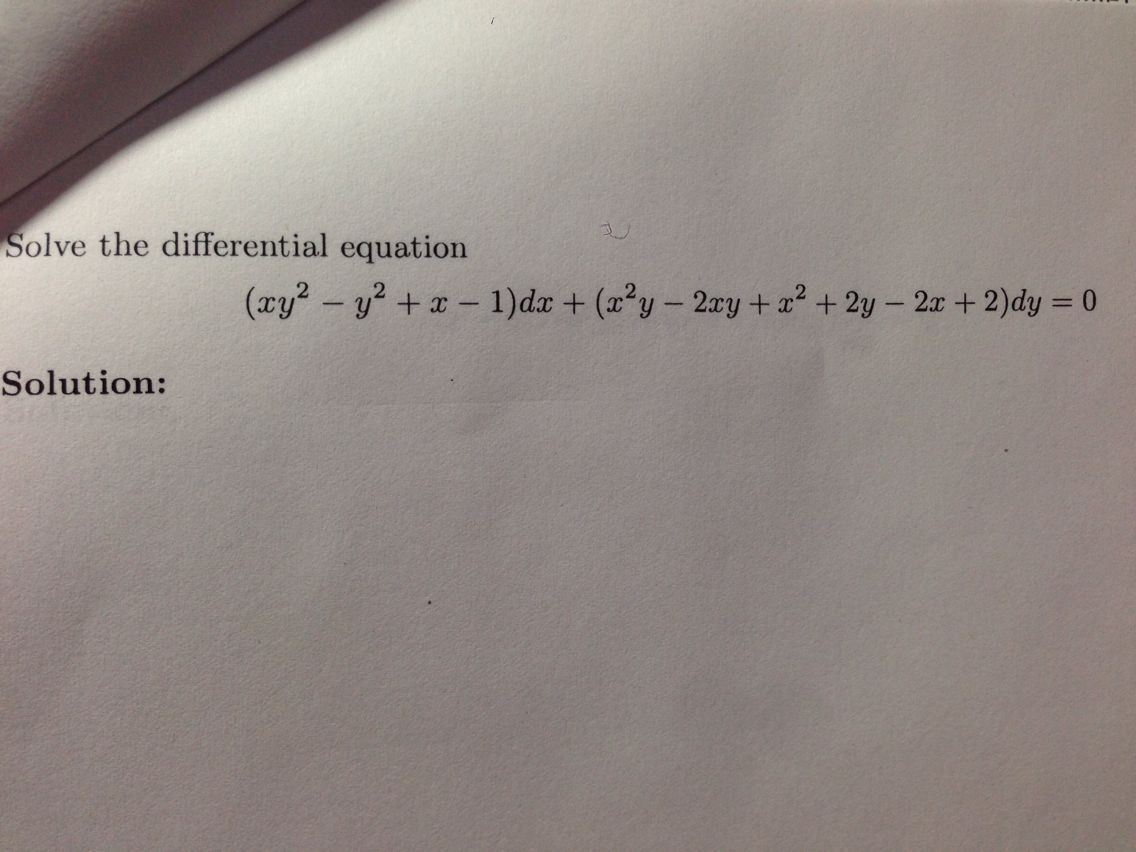 |  | |
 |  |  |
 |  |  |
 | ||
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
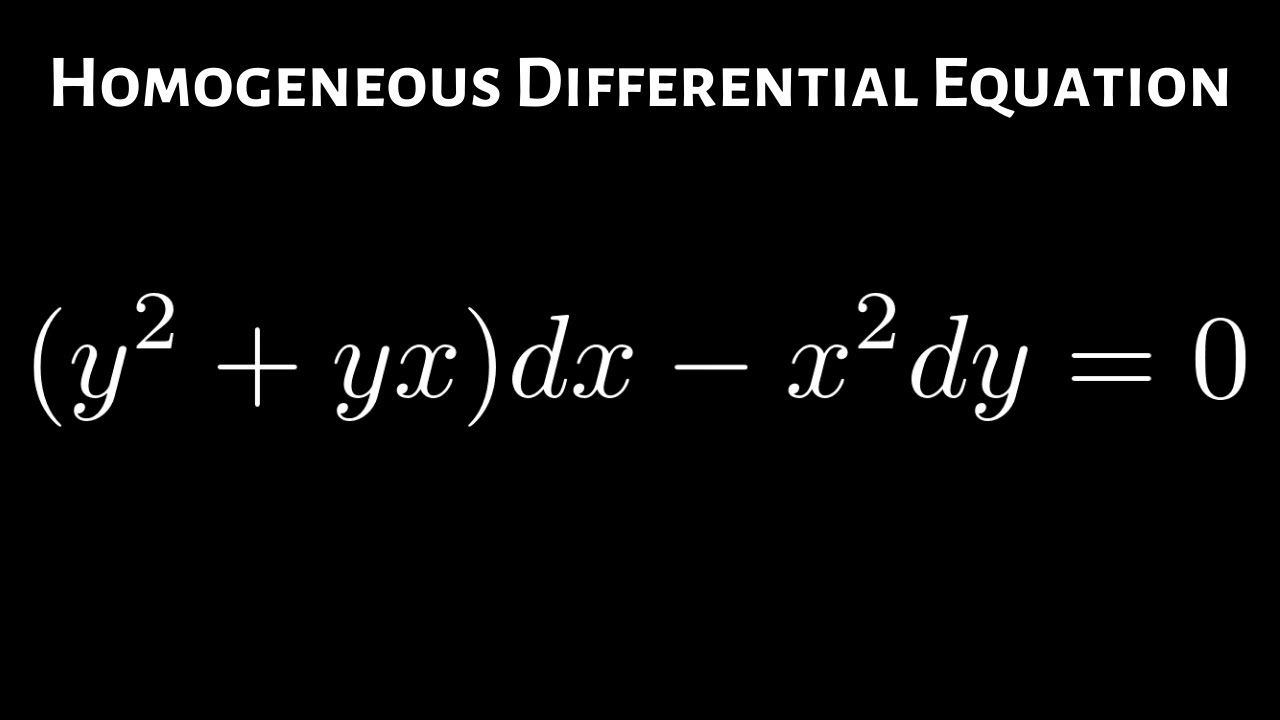 |  | |
 |  | |
 | ||
 |  | |
「X + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
Solve the following differential equation (x2 y2)dx 2xy dy = 0Answer (1 of 5) (1 y^2) dx (1 x^2)d y = 0 \implies (1 x^2) dy = (1 y^2)dx \implies \dfrac{dy}{1 y^2} = \dfrac{dx}{1 x^2} \text{integrating both
Incoming Term: x + y 2 dx + 2xy + x 2 − 1 dy 0 y 1 1,




0 件のコメント:
コメントを投稿